L'INVERSEUR DE PEAUCELLIER

La couverture des Malices du Kangourou/2001/Collèges montre un dispositif de dessin articulé, appelé inverseur, mis au point en 1864 par l'ingénieur Peaucellier : il permet de « transformer » des cercles en droites et inversement. Précisément, avec les notations de la figure, nous allons montrer ceci : quand le point M décrit un cercle, le point P décrit une droite ! Cette démonstration utilise des résultats connus en fin de collège.

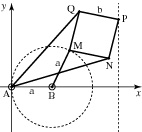
Les points A et B sont fixes, AN=AQ et MNPQ est un losange ; les points M, N, P, Q peuvent bouger avec les barres dont ils sont les extrémités articulées. Sur la figure, on a AB=BM=a et QP=b ; appelons t l'angle variable (Bx,BM). Prenons le système de coordonnées dont les axes sont Ax et Ay. Le point M décrit le cercle de centre B de rayon a ; et les points A, M, P restent alignés (en effet, M et P sont, comme A, sur la médiatrice de [QN]. Appliquons le théorème de Pythagore dans les triangles AOQ et POQ : QO2 = AQ2 – AO2 = PQ2 – PO2. Donc AO2 – PO2 = AQ2 – PO2. Les segments [AQ] et [PQ] étant de longueur constante, la différence AO2 – PO2 est constante. Mais elle vaut aussi (AO – PO)(AO + PO), c'est-à-dire AM.AP ; ce dernier produit reste donc égal à une constante K2. Les points A, M, P étant alignés, le produit AM.AP est aussi égal au produit scalaire des vecteurs AM et AP. Les coordonnées du vecteur AM sont (a+a.cost , a.sint). Et celles du vecteur AP sont donc (u.(a+a.cost) , u.a.sint) pour un certain u tel que AM.AP = K2. Le produit scalaire des vecteurs AM et AP vaut donc u.a2.(1+cost)2 + u.a2.sin2t = 2u.a2.(1+cost). On a donc u = K2 / [2a2.(1+cost)]. Les coordonnées du vecteur AP, et donc du point P, sont alors (K2/2a , K2sint / 2a(1+cost)). Le point P, ayant une abscisse constante décrit donc une droite perpendiculaire à (AB). CQFD.