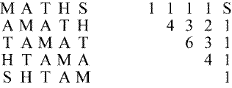Solutions du Kangourou de midi 2023

1) Réponse C.
Une araignée a 8 pattes, une mouche en a 6. Une pieuvre (octopode) a 8 tentacules, une seiche (décapode) en a 10. Cela fait 32, au total.

2) Réponse D.
Le 31 décembre 2023, Albert sait que son collègue et son père auront fêté leurs anniversaires dans l'année ; et alors l'année de naissance plus l'âge de l'un ou l'autre vaudra 2023. Et 2023+2023=4046.

3) Réponse C.
DIX vaut « cinq cent neuf » en chiffres romains.

4) Réponse C.
Le triangle de côté 3, 8, 5 est un triangle « plat », d'angles 180°, 0° et 0°.

5) Réponse E.
Les deux plus jeunes n'étaient pas nés il y a 7 ans.
Aujourd'hui, la somme des 3 plus vieux est 69 ans (80–5–6).
Il y a 7 ans, la somme de leurs âges valait 48 (69 – 3×7).

6) Réponse C.
La coïncidence ne peut arriver qu'une fois par jour et ne peut pas arriver si le jour est après le 23 du mois (car on passe de 23h59 à 00h00). Et elle arrive effectivement 23 jours par mois, ce qui fait 23×12, soit 276 fois (les premières et dernières fois étant 01h01 le 01/01 et 23h12 le 23/12).

7) Réponse A. 
Le mardi soir il y a 1+(2×1) avertis, soit 3. Le mercredi 3+(2×3) avertis, soit 9. Le jeudi 9+(2×9)=27=3³, le vendredi 3⁴=81, le samedi 3⁵=243 et le dimanche 3⁶=729. Autant d'hommes qu'il y a de feuilles à un « mille‑feuille » !

8) Réponse D.
64=12+24+24+4. Donc 64 heures après 12h00 le 1er avril, il sera 4h00 du matin le 4 avril. Et, à 4 heures du matin, à Paris, il fait nuit !
La probabilité d'ensoleillement est donc nulle.

9) Réponse E.
En partant des "M" pour aller jusqu'aux "S", le total des chemins est assez difficile à trouver. Par contre, on peut compter les nombres de chemins à rebours à partir d'un "S". Voici ces nombres à partir du S en haut à droite :

On trouve 1+4+6+4+1, soit 16 chemins.
On a 16 autres chemins pour le deuxième S (en bas à gauche).
Au total, cela fait 32 chemins, donc 32 manières d'écrire le mot MATHS.

10) Réponse E.
Les quatre nombres proposés sont possibles :
1, 2, 4, 8, 16
   est le début de la suite des diviseurs de 496 (… 31, 62, 124, 248, 496) ;
1, 2, 4, 8, 9, 12, 14, 15
   est le début de la suite des noms de nombres s'écrivant avec un « u » ;
1, 2, 4, 8, 17, 35, 71, 152
   est le début de la suite des puissances de 2 écrites en base 9 ;
1, 2, 4, 8, 7, 5, 10, 11, 13, 8
   est le début de la somme des chiffres des puissances de 2.

Retour au menu du jeu-concours Kangourou