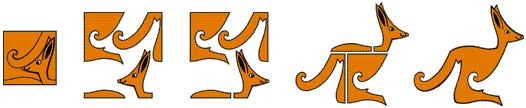|
KANGOUROU des mathématiques 2009 :
l'afficheTélécharger une affiche imprimable au format A4 :
Affiche "19 mars 2009" (pdf, 204 Ko)
Affiche non datée (pdf, 204 Ko)Cette affiche montre de belles mathématiques !
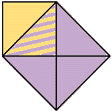
Le découpage suivant montre que le carré construit sur la diagonale d'un carré a une surface deux fois plus grande.
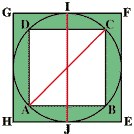
Le cercle, ayant pour diamètre la diagonale AC du (petit) carré, s'inscrit dans le carré de côté EF. En effet, AC = IJ et IJ = EF ; EF est bien le diamètre du cercle.
Le grand carré EFGH a donc même aire que celui construit sur la diagonale AC : il a une aire égale à deux fois celle du petit carré ABCD.
Donc Aire(EFGH) = Aire(ABCD) + Aire(ABCD).
Mais Aire(EFGH) = Aire(ABCD) + Aire(« couronne verte »).
La « couronne verte » a donc la même aire que le carré ABCD.
Et, dans la figure de l'affiche, le carré ABCD lui-même vaut deux fois le petit carré intérieur.
Et le petit carré intérieur peut se découper pour former le kangourou, qui a donc même aire que lui.
Finalement :
L'aire de la « couronne verte » est égale à deux fois l'aire du kangourou !