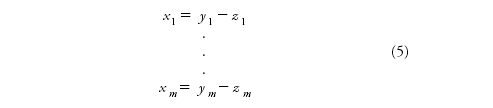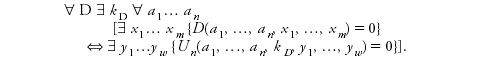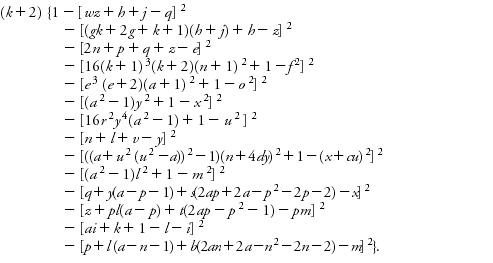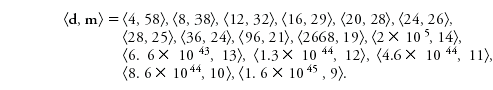 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
|||||||||||
(extrait de la recherche de la vérité)
Le dixième problème de Hilbert:
que peut-on faire avec les équations diophantiennes?
Yuri Matiiassévitch.
Professeur à l'Institut Steklov de mathématiques à Saint-Pétersbourg
J'ai déjà fait beaucoup d'exposés sur le dixième problème de Hilbert mais cela me fait très plaisir d'en faire un de plus à Paris, la ville dans laquelle David Hilbert a énoncé ses fameux problèmes. C'était pendant le Second Congrès International des Mathématiciens qui s'est tenu en 1900, c'est-à-dire la dernière année du dix-neuvième siècle.
Hilbert voulait signaler les plus importants problèmes mathématiques non résolus que le vingtième siècle allait hériter du dix-neuvième siècle. On parle habituellement des vingt-trois problèmes de Hilbert et on les nomme le premier, le second, le troisième, ..., le vingt-troisième problème d'après l'ordre dans lequel ils sont numérotés dans le texte publié. En fait plusieurs de ces problèmes sont des collections de problèmes ayant un lien entre eux. Par exemple le huitième problème comprend, en particulier :
• la conjecture de Goldbach,
• l'hypothèse de Riemann,
• l'infinitude des nombres premiers jumeaux.La formulation du dixième problème est si courte qu'elle peut être reproduite ici in extenso :
10. Entscheidung der Lösbarkeit einer diophantischen Gleichung.
Eine diophantische Gleichung mit irgendwelchen Unbekannten und
mit ganzen rationalen Zahl-koefficienten sei vorgelegt : man soll ein
Verfahren angeben, nach welchen sich mittels einer endlichen Anzahl von
Operationen entscheiden l”þt, ob die Gleichung in ganzen rationalen
Zahlen l–sbar ist.Une équation diophantienne est une équation de la forme :
où D est un polynôme à coefficients entiers, positifs ou négatifs. Ces équations sont appelées ainsi d'après le mathématicien grec Diophante qui vivait au troisième siècle.
Le dixième problème de Hilbert peut aussi être vu comme une collection de problèmes mais il existe une différence essentielle avec d'autres problèmes.
• Tout d'abord les problèmes individuels sont de même nature, chacun est représenté par une équation diophantienne particulière.
• Ensuite il existe un nombre infini (dénombrable) de tels problèmes.
• Enfin, et c'est le plus important, dans le dixième problème David Hilbert demande une méthode universelle unique qui doit pouvoir s'appliquer à chacune des équations. Depuis l'époque de Diophante, les théoriciens des nombres ont trouvé des solutions à un grand nombre d'équations diophantiennes, et ils ont établi aussi la non-résolubilité d'un grand nombre d'autres équations. Malheureusement, pour différentes classes d'équations, et même pour différentes équations particulières, il a été nécessaire d'inventer des méthodes spécifiques et différentes. Ce que demande Hilbert, c'est une méthode universelle pour décider de la résolubilité des équations diophantiennes.Dans la terminologie actuelle le dixième problème est un problème de décision, c'est-à-dire un problème qui se décompose en une infinité de problèmes particuliers qui demandent une réponse par OUI ou NON. Le cœur du problème de la décision est la recherche d'une méthode unique capable de fournir une réponse à tous ces problèmes particuliers.
Le dixième problème est le seul problème de décision parmi les 23 problèmes de Hilbert.
Dans son dixième problème, Hilbert pose la question de décidabilité à propos des solutions en entiers relatifs. On peut aussi considérer un problème analogue en cherchant des solutions en entiers naturels. Pour une équation diophantienne particulière, le problème de décider si elle a une solution entière et le problème de décider si elle a une solution positive sont en général deux problèmes vraiment distincts.
Par exemple l'équation :
a clairement une infinité de solutions de la forme x = z, y = - 1. D'autre part, le fait que cette équation n'ait pas de solutions positives x, y et z n'est pas trivial du tout.
D'autre part soit :
une équation diophantienne arbitraire ; supposons que nous soyons en train de chercher ses solutions entières x 1, ä, x m. Considérons l'équation :
Il est clair que toute solution de l'équation (4) d'entiers naturels y 1, ä, y m, z 1, ä, z m engendre la solution :
de l'équation (3) en entiers relatifs x 1, ä, x m. D'autre part, pour toute solution x 1, ä, x m de l'équation (3), on peut trouver des entiers naturels y 1, ä, y m, z 1, ä, z m satisfaisant (5) et donnant par conséquent une solution de l'équation (4). On dit que le problème d'existence de solutions en entiers relatifs pour l'équation quelconque (3) se réduit au problème d'existence de solutions en entiers naturels pour l'équation (4).
On dit aussi que le problème de décision d'existence de solutions en entiers relatifs se réduit au problème de décision d'existence de solutions en entiers naturels. En fait, ces deux problèmes sont équivalents mais la réduction en sens inverse est mois évidente.
Soit :
une équation diophantienne quelconque, et supposons que nous cherchions ses solutions positives. Considérons l'équation suivante :
Il est clair que toute solution de l'équation (7) en entiers relatifs fournit une solution de (6) en entiers positifs. La réciproque est tout aussi vraie, puisque, d'après un théorème de Lagrange, tout entier naturel peut être représenté comme somme de quatre carrés.
Ainsi nous avons montré que le problème de décision consistant à déterminer l'existence de solutions positives est réductible au problème de décision consistant à déterminer l'existence de solutions entières.
Nous avons vu que pour une équation diophantienne particulière, le problème de décider si elle a une solution entière et le problème de décider si elle a une solution positive sont en général deux problèmes vraiment distincts mais ces deux problèmes sont équivalents en tant que problèmes de décision, c'est-à-dire comme problèmes algorithmiques pour les classes des équations. Pour des raisons techniques, il est plus facile de travailler avec des variables de type entier naturel, et la plupart du temps je supposerai que nos inconnues sont des entiers positifs.
Une solution d'un problème de décision donné doit être donnée sous la forme d'un algorithme qui, pour une entrée donnée, doit toujours fournir la réponse désirée OUI ou NON. Cependant à la fin du dix-neuvième siècle, lorsque Hilbert posa son problème, il n'y avait pas de définition mathématique rigoureuse de ce qu'est un algorithme. Tout ce qui était connu étaient des exemples divers d'algorithmes, commenÁant avec l'algorithme d'Euclide pour déterminer le pgcd de deux entiers naturels. C'est pourquoi Hilbert, au lieu de la notion d'algorithme, utilisa une terminologie un peu plus vague en demandant "une méthode par laquelle, au moyen d'un nombre fini d'opérations, ...".
L'absence d'une définition générale de ce qu'est un algorithme n'était pas par elle-même un obstacle pour une solution positive du dixième problème. Si quelqu'un avait trouvé la "méthode" désirée il aurait été clair que cette méthode faisait bien le travail.
La situation est très différente s'il n'existe pas d'algorithme, comme cela se passe pour le dixième problème. Pour le montrer, ou même pour l'énoncer rigoureusement, nous avons besoin d'une définition de ce qu'est un algorithme.
Une telle définition fut donnée beaucoup plus tard, seulement dans les années 1930 avec les travaux de Kurt G–del, de Alan Turing, de Emil Post, de Alonzo Church et d'autres logiciens. Des modèles différents ont été introduits pour décrire les outils de calculs : le lambda-calcul, les fonctions récursives, les machines de Turing, etc. Alonzo Church a été le premier à comprendre que chacune de ces définitions particulières reflétait notre idée intuitive de la notion générale d'algorithme. Cette assertion est maintenant connue sous le nom de thèse de Church.
Aujourd'hui nous savons que le dixième problème de Hilbert n'a pas de solution. Ceci signifie qu'il est indécidable en tant que problème de décision.
Théorème (Indécidabilité du dixième problème de Hilbert).
Il n'existe pas d'algorithme qui, pour une équation diophantienne arbitraire donnée,
nous dit si l'équation a une solution ou non.On parle dans ce sens de la "solution négative" du dixième problème de Hilbert. En fait cette solution négative peut être énoncée sous une forme renforcée par rapport à celle énoncée ci-dessus. Pour démontrer seulement la non-existence de l'algorithme voulu on pourrait supposer l'existence d'un tel algorithme et en déduire une contradiction. Cette faÁon de faire ne donne rien de plus que la déduction de la contradiction.
Cependant, pour le dixième problème de Hilbert, nous pouvons faire un peu plus. La non-existence de l'algorithme pour le dixième problème de Hilbert signifie que, pour tout algorithme A supposant résoudre le dixième problème de Hilbert, il existe une équation particulière :
pour laquelle il ne donne pas la réponse exacte. Plus précisément pour ce contre-exemple soit l'algorithme ne s'arrête jamais, soit son résultat, s'il existe, est faux.
Théorème (Forme renforcée de l'indécidabilité du dixième problème de Hilbert).
Il existe un algorithme qui, pour un algorithme A donné, fournit un contre-exemple
à l'hypothèse que A résout le dixième problème de Hilbert.L'algorithme A peut être représenté sous n'importe quelle forme standard : comme une machine de Turing, comme une fonction récursive, ou comme un programme en Pascal sans variables de type real.
Ces formes de l'indécidabilité du dixième problème de Hilbert nous indiquent un lien très fort entre les algorithmes et les équations diophantiennes. L'existence d'un tel lien a été conjecturé au début des années 1950 par le mathématicien américain Martin Davis. Pour être capable d'énoncer cette hypothèse j'ai besoin d'introduire un peu plus de terminologie.
Au-delà des équations diophantiennes individuelles nous pouvons considérer aussi les familles d'équations diophantiennes. Une telle famille est définie par une équation diophantienne de la forme :
où D est un polynôme à coefficients entiers relatifs, les variables étant partagées en deux groupes :
• les paramètres a 1, ä, a n ;
• les inconnues x 1, ä, x m.
Je supposerai que les paramètres, ainsi que les inconnues, ne peuvent prendre que des valeurs positives. Pour certains choix de valeurs des paramètres a 1, ä, a n l'équation (9) possède une solution en les inconnues x 1, ä, x m ; pour d'autres choix des valeurs des paramètres elle n'a pas de solution. Nous pouvons considérer l'ensemble
des n-uplets (a 1, ä, a n) pour lesquels notre équation paramétrée possède une solution, c'est-à-dire :
De tels ensembles sont dits diophantiens. L'équivalence de la forme (10) s'appelle une représentation diophantienne de l'ensemple
Des exemples faciles d'ensembles diophantiens sont les suivants :
• l'ensemble des carrés parfaits, représenté par l'équation :
• l'ensemble des nombres composés, représenté par l'équation :
• l'ensemble des entiers naturels qui ne sont pas une puissance de 2, représenté par l'équation :
Il est un peu moins évident de montrer que l'ensemble des entiers naturels qui ne sont pas des carrés parfaits est aussi un ensemble diophantien. Il est cependant représenté par l'équation :
Si nous nous interrogeons sur le complément des deux autres ensembles, la réponse n'est pas claire du tout.
• L'ensemble des nombres premiers est-il diophantien ?
• L'ensemble des puissances de 2 est-il diophantien ?
Il est naturel de se demander s'il existe une caractérisation de la classe des ensembles diophantiens ou, tout au moins, de chercher des conditions nécessaires ou des conditions suffisantes pour qu'un ensemble soit diophantien. On trouve une condition nécessaire si on considère les ensembles diophantiens d'un point de vue algorithmique, c'est-à-dire comme calculables sur ordinateur. D'un point de vue algorithmique tous les ensembles diophantiens possèdent une propriété importante, à savoir qu'étant donnée une équation diophantienne (9) nous pouvons fournir de faÁon effective une liste des n-uplets de l'ensemble diophantien
L'algorithme que nous venons de décrire pour énumérer les ensembles diophantiens possède une forme très particulière. En permettant des algorithmes quelconques nous en arrivons à la notion suivante, étudiée en théorie de la calculabilité.
DÉFINITION. ã Un ensemble
Il est, par exemple, facile d'écrire un programme en Pascal qui pourrait imprimer, si nous disposions d'un temps infini, tous les nombres premiers ou toutes les puissances de 2. Les ensembles correspondants sont donc listables.
Nous avons vu que, pour qu'un ensemble
Conjecture de Martin Davis. ã Les notions d'ensemble diophantien et d'ensemble listable coïncident ; autrement dit un ensemble est diophantien si, et seulement si, il est listable.
La conjecture de Martin Davis énonce que des notions d'origines différentes, l'une provenant de la théorie des nombres et l'autre de la théorie de la calculabilité, correspondent en fait au même concept.
Cette conjecture était plutôt audacieuse car elle a beaucoup de conséquences étonnantes. Elle implique par exemple l'existence d'un polynôme P tel que l'équation :
possède une solution si, et seulement si, a est un nombre premier. Il fut noté par Hilary Putnam qu'une telle équation peut être réécrite de la faÁon suivante :
En fait toute solution de l'équation (15) peut être étendue en une solution de l'équation (16) en posant :
D'autre part, dans toute solution, à coordonnées positives, de l'équation (16), le produit doit être positif, ce qui n'est possible que si :
ce qui implique à la fois (15) et (17). La conjecture de Davis impliquait donc l'existence d'un polynôme particulier (le membre droit de (16)) tel que l'ensemble de ses valeurs positives est exactement l'ensemble de tous les nombres premiers :
Ce corollaire fut considéré par beaucoup de mathématiciens comme un argument (informel) contre la conjecture de Davis. Il existait encore un autre corollaire étonnant de la conjecture de Davis. Nous pouvons lister tous les ensembles listables :
De faÁon formelle, pour un n donné, nous pouvons considérer l'ensemble
des (n + 1)-uplets tels que :
Il n'est pas difficile de choisir une telle liste (20) d'ensembles listables de faÁon à ce que l'ensemble
L'équation (21) implique qu'une représentation diophantienne d'un ensemble listable quelconque de n-uplets peut être obtenue à partir d'un même polynôme donné
Les ensembles listables universels et d'autres objets semblables, comme les machines de Turing universelles, ont été étudiés depuis longtemps en théorie de la calculabilité. La conjecture de Davis impliquait l'existence d'un tel objet universel en Théorie des nombres, à savoir l'existence pour chaque entier naturel n d'une équation diophantienne universelle. Plus précisément, il résulte de (21) et de (22) que l'équation :
est universelle au sens suivant :
Pour chaque équation diophantienne (9) on peut effectivement trouver un entier k D tel que l'équation (9) possède une solution pour des valeurs données des paramètres si, et seulement si, l'équation (23) possède une solution pour les mêmes valeurs des paramètres a 1, ä, a n et cette valeur du paramètre k :
Rien d'analogue n'était connu en Théorie des nombres avant cela : on peut réduire de faÁon effective le problème consistant à résoudre une équation paramétrée de degré aussi grand que l'on veut avec autant d'inconnues que l'on veut au problème consistant à résoudre une autre équation avec les mêmes paramètres mais avec un degré fixé et un nombre d'inconnues fixé.
Dans le cas n = 1 nous pouvons appliquer le "truc" de Putnam une fois de plus et trouver un polynôme universel V(k, y 1, ä, y m). Pour tout ensemble listable M d'entiers naturels il existe un entier k M tel que M soit exactement l'ensemble de toutes les valeurs positives prises par V pour k = k M et des valeurs entières positives de y 1, ä, y m.
En particulier, pour un certain entier k, le polynôme V représente de cette faÁon l'ensemble de tous les nombres premiers, pour une autre valeur de k, l'ensemble de toutes les puissances de 2 et ainsi de suite. Martin Davis a effectué le premier pas de la démonstration de sa conjecture. Il a en effet démontré que tout ensemble listable M possède une représentation presque diophantienne.
Théorème (Martin Davis, 1950).
Tout ensemble listable M possède une représentation de la forme :
Les représentations du type ci-dessus devinrent connues sous le nom de forme normale de Davis. Elles diffèrent des représentations diophantiennes par la présence d'un seul quantificateur universel, qui en plus est borné. C'était une avancée quantitative par rapport au résultat classique de Kurt G–del qui avait démontré l'existence de représentations arithmétiques semblables avec un nombre quelconque de quantificateurs universels.
Tout ce qui restait à démontrer pour prouver la conjecture de Davis était d'éliminer le dernier quantificateur universel mais ceci prit vingt ans. Tout d'abord ce quantificateur universel fut éliminé dans un célèbre article cosigné par Martin Davis, Hilary Putnam et Julia Robinson publié en 1961. Cependant le coût de cette élimination était important. En effet Davis, Putnam et Robinson furent forcés de considérer une classe d'équations plus importante que celle des équations diophantiennes, appelée la classe des équations diophantiennes exponentielles. Ce sont les équations de la forme :
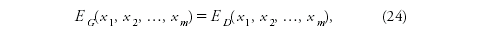
où E G et E D sont ce qu'on appelle des polynômes exponentiels, c'est-à-dire des expressions construites par les règles usuelles à partir des variables et des entiers naturels en utilisant l'addition, la multiplication et l'exponentiation.
Un exemple d'une telle équation diophantienne exponentielle est :
Davis, Putnam et Robinson ont obtenu une représentation diophantienne exponentielle de tout ensemble listable.
Théorème (Martin Davis, Julia Robinson, Hilary Putnam, 1961).
Pour tout ensemble listable
où E G et E D sont des polynômes exponentiels.
Ce fut une grande percée puisqu'ici nous avons une représentation purement existentielle et ainsi nous avons des corollaires immédiats sur les équations. On peut, en particulier, construire une équation diophantienne exponentielle universelle :
et ainsi le problème consistant à résoudre une équation diophantienne exponentielle quelconque peut être réduit au problème consistant à résoudre une équation diophantienne exponentielle avec un nombre fixé d'inconnues. Aujourd'hui nous savons que ce nombre d'inconnues peut être aussi petit que trois.
Une telle réduction est purement arithmétique dans son énoncé mais il semble qu'elle n'a jamais été suspectée par les théoriciens des nombres. Elle fut démontrée par des logiciens à l'aide de notions venant de la théorie de la calculabilité. Nous pouvons construire aujourd'hui une équation diophantienne exponentielle universelle par des moyens purement arithmétiques.
Mais, même après ce résultat remarquable de Davis, Putnam et Robinson, pour quelques logiciens éminents l'existence d'une équation diophantienne universelle semblait impossible. Ce qui suit fut écrit par George Kreisel dans la recension de l'article de Davis, Putnam et Robinson dans les Mathematical Reviews :
Ces résultats ne se rapportent que de faÁon superficielle au dixième problème de Hilbert sur les équations diophantiennes (ordinaires, c'est-à-dire non-exponentielles). La démonstration des résultats des auteurs, quoique très élégante, n'utilise pas de faits profonds de la théorie des nombres, ni de la théorie des ensembles r. e. (récursivement énumérables), et il est également probable que le présent résultat n'est pas intimement lié au dixième problème de Hilbert. Aussi, n'est-il pas entièrement plausible que tous les problèmes diophantiens (ordinaires) soient uniformément réductibles à ces derniers, lorsque le nombre de variables et le degré sont fixés, ce qui serait le cas si tous les ensembles r. e. étaient diophantiens.
Après le travail de Davis, Putnam et Robinson pour essayer de démontrer la conjecture de Davis, il était suffisant de montrer que l'ensemble de tous les triplets de la forme (a, b, a puissance b) est diophantien. En effet supposons qu'il en soit ainsi. Soit alors :
la représentation diophantienne correspondante. à l'aide d'un tel polynôme A nous pouvons transformer une équation diophantienne exponentielle quelconque en une équation diophantienne avec des inconnues supplémentaires. Considérons à nouveau l'équation (25). Nous avons ici trois exponentiations. Nous pouvons utiliser trois copies de l'équation diophantienne (27) pour transformer l'équation (25) en l'équation :
En d'autres mots, afin de prouver que chaque ensemble listable possède une représentation diophantienne il est suffisant de démontrer qu'un ensemble listable particulier de triplets est diophantien. En fait l'étude de ce problème particulier commenÁa beaucoup plus tôt avec Julia Robinson, au début des années 1950, c'est-à-dire au moment même où Martin Davis posa sa conjecture.
Julia Robinson échoua dans sa tentative de trouver une représentation (27) de l'exponentiation. Elle trouva cependant des conditions suffisantes pour l'existence d'une telle représentation.
Théorème (Julia Robinson, 1952).
Il existe un polynôme A tel que :
pourvu qu'il existe une équation :
telle que :
• pour toute solution de l'équation nous avons u < v puiss v ;
• pour tout k il existe une solution vérifiant u > v puiss k.
L'équation (28) définit une relation entre u et v qui est réalisée si, et seulement si, l'équation (28) possède une solution. Julia Robinson appela relation à croissance exponentielle une telle relation satisfaisant ces deux conditions. Elles devinrent connues dans la littérature sous le nom de relations de Julia Robinson.
Il reste donc, pour démontrer la conjecture de Davis, à trouver une relation à croissance exponentielle définie par une équation diophantienne. De faÁon surprenante, parmi les nombreuses équations à deux paramètres étudiées en Théorie des nombres, depuis Diophante jusqu'à la fin des années 1960, aucune ne définit une relation à croissance exponentielle.
Ce fait, ainsi que les conséquences étonnantes de la conjecture de Davis, engendrèrent des doutes sérieux sur l'existence d'une relation de Julia Robinson. Elle-même, quelquefois, se mit à douter et commenÁa à chercher une solution positive au dixième problème de Hilbert.
Enfin, en 1970, je fus capable de construire une équation définissant une relation à croissance exponentielle. Il s'agit de la relation :
où F 0, F 1, ä est la suite bien connue des nombres de Fibonacci :
0, 1, 1, 2, 3, 5, 8, 13, 21, ä
Cette célèbre suite a été très étudiée depuis l'époque de Fibonacci mais néanmoins j'ai trouvé une propriété remarquable qui semble être restée inconnue aux théoriciens des nombres pendant des siècles, à savoir que :
Cette propriété n'est pas difficile à démontrer une fois qu'elle a été énoncée.
La construction complète de la relation diophantienne à croissance exponentielle n'utilise pas de résultats profonds de la Théorie des nombres du vingtième siècle. Elle aurait pu être trouvée au siècle dernier. Ce qui manquait était une motivation.
Une telle motivation était alors une démonstration de la conjecture de Davis. Ma construction d'une relation à croissance exponentielle se trouva être chronologiquement la dernière étape de la preuve de la conjecture de Davis, souvent appelé le théorème DPRM d'après Davis-Putnam-Robinson-Matiiassévitch.
Théorème DPRM.
Tout ensemble listable
pour un certain polynôme D à coefficients entiers.
Ce théorème, ainsi que sa démonstration complète, peuvent être trouvés de nos jours dans plusieurs publications, y compris en langue franÁaise.
Nous avons obtenu, avec la preuve de la conjecture de Davis, tous les corollaires improbables. La preuve complète est constructive en ce sens que, étant donnée une représentation standard d'un ensemble listable, nous pouvons trouver de faÁon effective une de ses représentations diophantiennes. Nous pouvons, par exemple, obtenir la représentation polynomiale de l'ensemble des nombres premiers.
Théorème.
L'ensemble des nombres premiers est égal à l'ensemble des valeurs strictement positives prises par le polynôme :
avec des valeurs strictement positives des 26 variables a, ä, z.
Toutes les lettres de l'alphabet sont utilisées ici. Aujourd'hui, on peut construire une représentation polynomiale des nombres premiers avec seulement dix variables.
Revenons au dixième problème de Hilbert. La conjecture de Davis implique son indécidabilité, et même en un sens très fort. Un résultat classique de la théorie de la calculabilité est l'existence d'un ensemble listable W indécidable d'entiers naturels. Pour cet ensemble il n'existe aucun algorithme pour déterminer, pour un entier naturel a, s'il appartient à cet ensemble ou non. Puisque W est un ensemble listable, nous pouvons trouver une de ses représentations diophantiennes :
L'indécidabilité de W implique qu'il n'existe pas d'algorithme pour déterminer pour quelles valeurs de a l'équation (32) possède une solution et pour quelles valeurs elle n'en possède pas.
Théorème (Une autre forme forte de l'indécidabilité du dixième problème de Hilbert).
Il existe une équation diophantienne à un seul paramètre :
pour laquelle il n'existe pas d'algorithme pour déterminer, pour une valeur donnée de a, si cette équation possède une solution en entiers naturels x 1, ä, x m.
Ainsi nous n'avons pas besoin de considérer la classe complète de toutes les équations diophantiennes pour obtenir un résultat d'indécidabilité. Il suffit de considérer seulement les équations de degré majoré par un certain nombre d et avec un nombre d'inconnues majoré par un autre nombre m.
Il existe un compromis entre ces deux bornes, c'est-à-dire que l'une peut être rendue plus petite au coût de l'accroissement de l'autre. Les records actuels sont les suivants :
Nous avons vu deux formes fortes de l'indécidabilité du dixième problème de Hilbert. Nous pouvons les considérer en une seule fois.
Théorème (Forme la plus forte de l'indécidabilité du dixième problème de Hilbert).
Il existe un algorithme qui, pour un algorithme donné, fournit un entier
tel que l'algorithme
Cette forme fournit une solution négative au dixième problème de Hilbert. Hilbert lui-même l'accepterait-il comme solution? Je pense que "OUI". Pour justifier ce point de vue je désire citer une partie du célèbre article de Hilbert :
Il se peut aussi que l'on s'efforce d'obtenir une solution en se basant sur des hypothèses insuffisantes ou mal comprises et que, par suite, on ne puisse atteindre le but. Il s'agit alors de démontrer l'impossibilité de résoudre le problème en se servant d'hypothèses telles qu'elles ont été données ou interprétées. Les Anciens nous ont donné les premiers exemples de pareilles démonstrations d'impossibilité ; ils ont démontré ainsi que dans un triangle rectangle isocèle l'hypoténuse et le côté de l'angle droit sont dans un rapport irrationnel. Dans les Mathématiques contemporaines, la question de l'impossibilité de certaines solutions joue un rôle prépondérant ; c'est à ce point de vue de la démonstration de l'impossibilité que d'anciens et difficiles problèmes, tels que ceux de la démonstration de l'axiome des parallèles, de la quadrature du cercle et de la résolution par radicaux de l'équation du cinquième degré, ont reÁu une solution parfaitement satisfaisante et rigoureuse, bien qu'en un sens tout différent de celui qu'on cherchait primitivement. Le fait remarquable dont nous venons de parler et certains raisonnements philosophiques ont fait naître en nous la conviction que partagera certainement tout mathématicien, mais que jusqu'ici personne n'a étayée d'aucune preuve, la conviction, dis-je, que tout problème mathématique déterminé doit être forcément susceptible d'une solution rigoureuse, que ce soit par une réponse directe à la question posée, ou bien par la démonstration de l'impossibilité de la résolution, c'est-à-dire la nécessité de l'insuccès de toute tentative de résolution.
Ainsi, presque certainement, Hilbert serait satisfait de la "solution négative" du dixième problème. Mais nous pouvons désormais nous poser une autre question : Hilbert serait-il satisfait de l'énoncé du problème lui-même s'il avait su qu'il pouvait être "résolu" de cette faÁon? Je pense que "NON".
J'explique mon point de vue. Le dixième problème occupe moins d'espace qu'aucun autre problème dans l'article de Hilbert. Durant son exposé il n'en dit pas un mot, ainsi que sur quelques autres problèmes. Son exposé dura deux heures et demi mais ceci ne fut pas suffisant pour présenter les vint-trois problèmes ; ainsi quelques problèmes, dont le dixième, ne furent pas présentés oralement mais seulement inclus dans la version imprimée de l'exposé.
Ainsi Hilbert ne donna-t-il pas de motivation pour le dixième problème. Nous pouvons seulement deviner pourquoi il ne parla que des solutions en "entiers rationnels". Nous avons vu que cela est équivalent à rechercher un algorithme pour résoudre les équations diophantiennes en entiers naturels. Mais, en fait, Diophante lui-même ne résolvait les équations ni en entiers naturels, ni en entiers relatifs, il cherchait des solutions rationnelles. Donc pourquoi Hilbert ne demanda-t-il pas une procédure pour déterminer l'existence de solutions rationnelles? La réponse est plus ou moins évidente. Hilbert était optimiste et croyait en l'existence d'un algorithme pour résoudre les équations diophantiennes en entiers. Un tel algorithme nous permettrait également de résoudre les équations en rationnels.En effet, résoudre une équation :
en les rationnels c 1, ä, c m est équivalent à résoudre l'équation :
en les entiers naturels x 1, ä, x m, y 1, ä, y m, z. La dernière équation est équivalente à l'équation diophantienne :
où d est le degré de D.
Il existe une réduction un peu moins évidente de la résolution des équations diophantiennes en rationnels à la résolution des équations diophantiennes homogènes en entiers. Nous commenÁons par transformer (34) en :
et alors en :
mais un "truc" supplémentaire est nécessaire pour garantir que z est différent de zéro.
Ainsi en demandant explicitement de résoudre les équations diophantiennes en entiers, Hilbert demandait implicitement de résoudre les équations diophantiennes en rationnels. Une solution positive du dixième problème, tel qu'il fut énoncé, aurait donné immédiatement une solution positive au problème analogue sur les solutions en rationnels.
Cependant nous avons obtenu une solution négative de l'énoncé originel du dixième problème. Qu'est-ce que cela implique pour la résolution des équations diophantiennes en rationnels ? Rien. En fait le problème de décision de détermination de la résolution d'une équation diophantienne quelconque en rationnels est équivalent au problème de la résolution des équations diophantiennes homogènes en entiers. De telles équations forment seulement une sous-classe de l'ensemble des équations diophantiennes et il est en fait possible que pour cette classe réduite il existe un algorithme.
Ainsi, très certainement, si Hilbert avait pressenti l'inexistence d'un algorithme pour résoudre les équations diophantiennes en entiers, il aurait également inclus dans le dixième problème le cas de la résolution en rationnels. Nous pouvons donc comprendre le dixième problème en deux sens.
• Le sens restreint, c'est-à-dire le problème tel qu'il a été littéralement énoncé.
• Le sens large, incluant d'autres problèmes dont la solution aurait suivi facilement d'une solution positive du dixième problème tel qu'il a été énoncé.
Dans le sens restreint le dixième problème est clos mais dans le sens large il est encore ouvert.
Résoudre des équations reste un des plus importants problèmes ouverts à propos du dixième problème pris dans son sens large. Les progrès dans cette direction sont plutôt faibles.
D'autres problèmes ouverts existent. Au lieu de résoudre les équations diophantiennes en rationnels, on peut être intéressé à les résoudre en l'anneau des entiers d'une extension algébrique du corps des rationnels. On peut, par exemple, être intéressé à résoudre les équations diophantiennes en entiers de Gauss, c'est-à-dire les nombres de la forme a + b.i avec a, b
Il est clair qu'une équation :
possède une solution en entiers de Gauss si, et seulement si, l'équation :
possède une solution en entiers relatifs. En écrivant :
nous pouvons réduire la résolution de l'équation (39) en entiers de de Gauss à la résolution de l'équation diophantienne :
en entiers.
Ainsi pouvons-nous considérer les équations diophantiennes en entiers de Gauss comme une partie du dixième problème de Hilbert au sens large.
Ce problème a été montré indécidable par Denef. Plus précisément il a trouvé une réduction dans le sens opposé, c'est-à-dire qu'il a montré comment le problème consistant à résoudre une équation diophantienne :
en entiers peut être réduit au problème consistant à résoudre une autre équation diophantienne :
en entiers de Gauss. Gr’ce à cette réduction, l'indécidabilité du dixième problème dans le sens restreint implique l'indécidabilité de sa contre-partie pour les entiers de Gauss.
Des réductions semblables ont été trouvées par différents chercheurs pour les anneaux d'entiers de quelques autres extensions algébriques du corps des rationnels, ce qui constitue un progrès pour le dixième problème de Hilbert au sens large. Cependant ceci n'a été fait que pour certaines extensions bien particulières, le cas général d'une extension quelconque reste encore un important problème ouvert à propos du dixième problème au sens large.
En introduisant le problème au sens large j'ai parlé de "problèmes de décision dont la solution aurait suivie facilement d'une solution positive du dixième problème tel qu'il a été énoncé". La résolution des équations diophantiennes en rationnels ou en entiers de Gauss aurait suivi facilement. Il existe beaucoup d'autres problèmes dont la réduction au dixième problème n'est pas difficile mais beaucoup moins évidente. Je vais maintenant présenter plusieurs exemples de tels problèmes qui peuvent être considérés comme des cas du dixième problème au sens large.
CommenÁons par le célèbre dernier théorème de Fermat qui vient d'être résolu. Hilbert n'inclut pas explicitement le dernier théorème de Fermat dans ses problèmes. Ce problème concerne la non-résolubilité d'un ensemble infini d'équations diophantiennes :
et donc il n'apparaît pas a priori comme un cas du dixième problème puisque Hilbert demandait seulement la solution d'équations diophantiennes simples et non pas d'une famille d'entre elles.
L'équation de Fermat est une équation diophantienne en x, y et z pour une valeur fixée de n mais est une équation diophantienne exponentielle si on la regarde comme une équation en x, y, z et n. Mais maintenant nous savons comment transformer une équation diophantienne exponentielle en une équation diophantienne véritable avec des inconnues supplémentaires. Nous pouvons construire, en particulier, un polynôme F à coefficients entiers tel que l'équation :
possède une solution en u 1, ä, u m si, et seulement si, n, x, y et z forment une solution de l'équation de Fermat. Ainsi le dernier théorème de Fermat est-il équivalent à l'énoncé disant qu'une certaine équation diophantienne véritable :
ne possède pas de solution en les inconnues en entiers naturels. Quelqu'un a pris soin d'exhiber une telle équation explicitement. Ainsi une solution positive au dixième problème de Hilbert dans sa formulation originelle nous aurait donné un outil pour confirmer ou infirmer le dernier théorème de Fermat. Ainsi, bien que le dernier théorème de Fermat ne soit pas présenté explicitement parmi les problèmes de Hilbert, il est présenté comme un cas très particulier du dixième problème.
Cependant une telle réduction du dernier théorème de Fermat à une seule équation diophantienne n'était pas connue avant 1970.
Nous pouvons considérer un autre problème célèbre, la conjecture de Golbach, qui a été incluse par Hilbert dans son huitième problème et qui demeure toujours ouvert.
La conjecture de Goldbach dit que tout entier pair plus grand que quatre est la somme de deux nombres premiers. Nous pouvons considérer l'ensemble
qui possède une solution si, et seulement si, a ne vérifie pas la conjecture. La conjecture de Goldbach est équivalente à l'énoncé disant que l'ensemble
n'a pas de solution du tout.
Nous voyons une fois de plus que la solution positive au dixième problème sous sa forme originelle nous aurait permis de savoir si la conjecture de Goldbach est vraie ou non.
La réduction de la conjecture de Goldbach à une équation diophantienne particulière est moins évidente et requière plus de technique que la réduction du dernier théorème de Fermat puisque nous avons désormais à faire à la primalité. Cette réduction n'est peut-être pas étonnante puisque la conjecture de Goldbach concerne les entiers naturels.
À part la conjecture de Goldbach, Hilbert inclut dans son huitième problème une autre conjecture, la célèbre hypothèse de Riemann. Dans sa formulation originelle c'est un énoncé sur les zéros complexes de la fonction dzéta de Riemann, qui est le prolongement analytique de la série :
qui converge pour R(z) . 1. Néanmoins nous pouvons21 construire une équation diophantienne particulière :
qui ne possède pas de solution si, et seulement si, l'hypothèse de Riemann est vraie. Une telle réduction exige soit l'utilisation de la théorie des fonctions analytiques, soit l'utilisation du fait que l'hypothèse de Riemann peut être reformulée comme un énoncé sur la distribution des nombres premiers.
Ainsi voyons-nous une fois de plus qu'un problème mathématique est un cas particulier du dixième problème de Hilbert dans sa forme originelle. Les trois célèbres problèmes considérés ci-dessus, c'est-à-dire le dernier théorème de Fermat, la conjecture de Goldbach et l'hypothèse de Riemann, concernent les entiers et donc leur réduction à des équations diophantiennes, bien que non évidente, est tout à fait imaginable a priori. Cependant, en Logique mathématique il existe un outil puissant, l'arithmétisation, qui nous permet de réduire à la théorie des nombres des problèmes qui ne portent pas sur les entiers du tout. Comme dernier exemple je vais considérer un célèbre défi aux mathématiciens, le problème des quatre couleurs, résolu en 1976 par Appel et Haken. C'est un problème sur la coloration des cartes planes mais, une fois de plus, nous pouvons construire une équation diophantienne :
qui ne possède pas de solution si, et seulement si, le problème des quatre couleurs est vrai. Une fois encore un problème qui n'a pas été inclus par Hilbert dans sa liste de problèmes apparaît comme une forme masquée du dixième problème.
J'ai décrit la réduction à des équations diophantiennes de quatre problèmes célèbres :
• le dernier théorème de Fermat,
• la conjecture de Goldbach,
• l'hypothèse de Riemann,
• le problème des quatre couleurs.
Deux de ces problèmes sont maintenant résolus, les deux autres restant ouverts. Ces réductions nous donnent une "preuve psychologique" de l'indécidabilité du dixième problème de Hilbert, puisqu'il est impensable qu'une seule méthode nous permette de résoudre automatiquement plusieurs problèmes tellement divers et très profonds. La réduction de ces problèmes peut être considérée comme amusante mais ces réductions sont-elles utiles? Le dixième problème est indécidable aussi n'avons-nous pas de méthode universelle pour résoudre tous les problèmes une fois pour toutes. Nous ne pouvons guère résoudre chacun de ces problèmes en regardant l'équation diophantienne particulière correspondante puisqu'elles sont plutôt compliquées.
Mais nous pouvons renverser l'ordre des choses. Le dixième problème est indécidable et nous avons besoin d'inventer de plus en plus de méthode ad hoc pour résoudre de plus en plus d'équations diophantiennes. Nous pouvons maintenant regarder la preuve du dernier théorème de Fermat et celle de la conjecture des quatre couleurs comme des outils très profonds pour traiter des équations diophantiennes particulières et nous pouvons essayer d'étendre ces techniques à d'autres équations.
Remerciements
L'auteur est très reconnaissant envers Patrick Cegielski pour son aide lors de la préparation en franÁais à la fois de l'exposé et de cet article.
Références
[1] K. Appel, W. Haken. Every planar map is four colorable, Illinois J. of Mathematics, 21/3 (1977), 429-490.
[2] Jean-Pierre Azra, Relations diophantiennes et la solution négative du 10e problème de Hilbert, Lecture Notes in Mathematics, 244 (1971), 11-28.
[3] Egon B–rger. Computability, Complexity, Logic (Amsterdam : North-Holland, 1989).
[4] Martin Davis, Arithmetical problems and recursively enumerable predicates. J. Symbolic Logic, 18/1 (1953), 33-41.
[5] Martin Davis, Hilbert's tenth problem is unsolvable. Amer. Math. Monthly, 80/3 (1973), 233-269 ; reprinted in : Martin Davis, Computability and Unsolvability.(New York : Dover Publications, 1982).
[6] Martin Davis, Yuri Matijasevich and Julia Robinson, Hilbert's tenth problem. Diophantine equations : positive aspects of a negative solution, in Mathematical Developments Arising from Hilbert Problems (F.E. Browder, ed.), Proc. Symp. Pure Math. 28 (1976), 323-378 ; reprinted in Solomon Feferman, ed., The collected works of Julia Robinson, American Mathematical Society, 1996, 269-324.
[7] Martin Davis, Hilary Putnam and Julia Robinson, The decision problem for exponential Diophantine equations, Ann. Math. (2) 74 (1961), 425-436 ; reprinted in The collected works of Julia Robinson, 77-88.
[8] Jan Denef, Hilbert's Tenth Problem for quadratic rings. Proceedings of the American Mathematical Society, 48/1 (1975), 214-220.
[9] Kurt G–del, Ðber formal unentscheidbare S”tze der Principia Mathematica und verwandter Systeme. I. Monatsh. Math. und Phys., 38/1 (1931), 173-198. Traduction anglaise dans Collected Works, vol. 1, Oxford University Press, 1986. Traduction franÁaise dans Le théorème de G–del, Seuil, 1989, 184 p., 105-143.
[10] David Hilbert, Mathematische Probleme. Vortrag, gehalten aufdem internationalen Mathematiker Kongress zu Paris 1900, Nachr. K.Ges. Wiss., G–ttingen, Math.-Phys.Kl. (1900), 253-297. Voir aussi Arch. Math. Phys. (1901) 44-63, 213-237. Voir aussi David Hilbert, Gesammelte Abhandlungen (Berlin : Springer, vol. 3 (1935)) ; (Reprinted : New York : Chelsea (1965)). Traduction franÁaise avec corrections et additions : Compte rendu du Deuxième Congrès International des Mathématiciens tenu à Paris du 6 au 12 août 1900, Gauthier-Villars, 1902, pp. 58-114 (réédition de la conférence de Hilbert : Paris : Editions Gabay, 1992). English translation : Bull. Amer. Math. Soc. (1901-1902) 437-479. Reprinted in : Mathematical Developments arising from Hilbert problems, Proceedings of symposia in pure mathematics, vol.28 (1976), 1-34.
[11] James P. Jones, Juri V. Matijasevich, A new representation for the symmetric binomial coefficient and its applications. Les Annales des Sciences Mathématiques du Québec, 6/1 (1982), 81-97.
[12] James P. Jones, Yuri V. Matijasevich, Proof of recursive unsolvability of Hilbert's tenth problem. Amer. Math. Monthly 98/8 (1991), {689-709}.
[13] James P. Jones, Daihachiro Sato, Hideo Wada, and Douglas Wiens, Diophantine representation of the set of prime numbers. The American Mathematical Monthly, 83/6 (1976), 449-464.
[14] George Kreisel, "Davis, Martin; Putnam, Hilary; Robinson, Julia. The decision problem for exponential Diophantine equations." Mathematical Reviews, 24#A3061: 573, 1962.
[15] Yuri I. Manin, A Course in Mathematical Logic. (New York; Heidelberg; Berlin : Springer, 1977).
[16] Maurice Margenstern, Le théorème de Matiyassévitch et résultats connexes, Lecture Notes in Mathematics, 890 (1981), 198-241.
[17] Yuri V. Matiiassévitch, Diofantovost' perechislimykh mnozhestv Dokl. AN SSSR, 191/2 (1970), 278-282. Traduit en anglais dans : Soviet Math. Doklady, 11/2 (1970), 354-358.
[18] Yuri Matiiassévitch, Diofantovy mnozhestva. Uspekhi Mat. Nauk, 27/5(167) (1972), {185-222}. Traduit en anglais dans : Russian Mathematical Surveys, 27/5 (1972), 124-164.
[19] Yuri Matiiassévitch, Prostye chisla perechislyayutsya polinomom ot 10 peremennykh. Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta im., V. A., Steklova AN SSSR , 68 (1977), 62-82. (Traduit en anglais dans : Journal of Soviet Mathematics, 15/1 (1981), 33-44.)
[20] Yuri V. Matiiassévitch, Algorifmicheskaya nerazreshimost 'èksponentsial' no diofantovykh uravnenii stremya neizvestnymi. Issledovaniya po teorii algorifmov i matematiheskoii} logike, A. A. Markov and V. I. Homich, Editors, Akademiya Nauk SSSR, Moscow 3: 69-78,1979. Traduit en anglais dans : Selecta Mathematica Sovietica, 3(3) : 223-232,1983/84.
[21] Yuri Matiiassévitch, Desyataya Problema Gilberta. Moscow, Fizmatlit, 1993. English translation : Hilbert's tenth problem. MIT Press, 1993. Traduction franÁaise : Le dixième problème de Hilbert, Masson, 1995
[22] Yuri Matiiassévitch, Les équations-bricoleurs. Revue de Mathématiques Spéciales, 5:305-309, 1994.
[23] Thanases Pheidas, Extensions of Hilbert's tenth problem. J. Symbolic Logic 59 : 2(1994),372-397.
[24] Hilary~Putnam, An unsolvable problem in number theory. J. Symbolic Logic, 25(3) : 220-232, 1960.
[25] Julia Robinson, Existential definability in arithmetic, Trans. Amer. Math. Soc. 72 (1952), 437-449. Reprinted in The collected works of Julia Robinson, 47-70.
[26] Craig Smorynski, Logical number theory I : An Introduction, Berlin, Springer-Verlag, 1991.
[27] Site consacré au dixième problème de Hilbert : URL : http://logic.pdmi.ras.ru/Hilbert10. (en anglais).
Hébergement : Cogitel